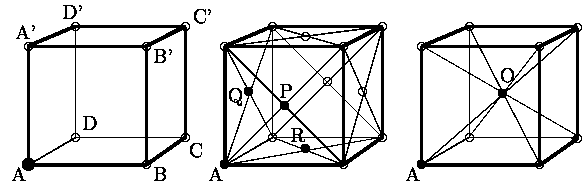
Обычно, знакомство с кристаллической структурой начинают с рассмотрения кубических примитивной, объемно- и гранецентрированной решеток (рис. 2.1), или, сокращенно, ПК, ОЦК, ГЦК.

Рис. 2.
1. Элементарные ячейки кубических решеток: а) простой; б) гранецентрированной; в) объемно--центрированнойКоординаты узлов этих ячеек соответственно равны:
|
ПК |
[[0, 0, 0]] |
|
ОЦК |
[[0, 0, 0]], [[1/2, 1/2, 1/2]] |
|
ГЦК |
[[0, 0, 0]], [[1/2, 1/2, 0]], [[1/2, 0, 1/2]], [[0, 1/2, 1/2]] |
Следует особо оговорить, какие именно частицы принадлежат ячейке, чтобы не учитывать одни и те же по нескольку раз, т.к. каждая грань является общей для двух параллелепипедов, ребро -- для четырех, а вершина -- для восьми. Поскольку грань ABCD (рис. 2.2а) переходит в A'B'C'D' при переносе на вектор
AA', будем считать, что, например, грань ABCD принадлежит ячейке, а A'B'C'D' --- нет. Рассуждая аналогично, приходим к выводу, что под элементарной ячейкой нужно понимать следующее:1) весь внутренний объем параллелепипеда;
2) одну вершину, например, A;
3) три непараллельных ребра, например, выходящие из этой вершины: AA', AB, AD (без точек A',B, D);
4) три непараллельные грани --- ABCD, ABB'A', ADD'A' --- только с перечисленными выше ребрами (без границы).
Так, для простой решетки достаточно одной вершины, например, A. Для объемно-центрированной --- вершины A и центра ячейки O. Для гранецентрированной --- вершины A и трех центров граней P, Q, R из шести (рис.2.
1). Таким образом, задав три элементарные трансляции a, b, c и необходимое количество n векторов частиц в ячейке (базис) {Pi, i=1┘n}, получаем множество векторов всех частиц кристалла r:|
r = k a + l b + m c + Pi |
i = {1 ┘ n }, m,n,p Î Z |
(2.1) |
здесь
Z --- множество целых чисел. Такие же обозначения мы будем использовать в дальнейшем и для других решеток.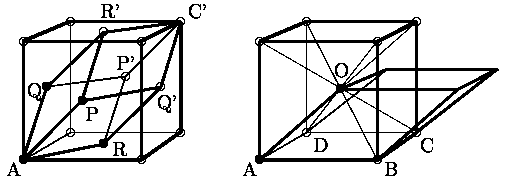
Рис. 2.
2. Минимальные элементарные ячейки кубических решеток: а) гранецентрированной; б) объемно--центрированнойОтметим также, что для объемно- и гранецентрированной решеток можно ввести элементарную ячейку и другим способом, так, чтобы она содержала всего один узел.
Как несложно заметить, вся гранецентрированная решетка переходит в себя при переносе на вектора, проведенные из угла ячейки в середины граней куба. Таким образом, параллелепипед (а точнее, ромбоэдр) APR'QRQ'C'R' на рис. 2.
2, построенный на этих векторах будет минимальной элементарной ячейкой решетки, содержащей всего один узел.Аналогично можно построить минимальную ячейку для объемно--центрированной решетки. Такой ячейкой может служить, например, параллелепипед, построенный на трех векторах AB, AD, AO.Однако, для ОЦК и ГЦК принято и более удобно работать с кубической ячейкой, несмотря на то, что она содержит несколько частиц. При этом лучше видны основные свойства симметрии и проще выполнять расчеты.
Простая гексагональная решетка
состоит из треугольных призм, в основании которых лежат правильные треугольники и имеет ось симметрии шестого порядка, то есть переходит в себя при поворотах на угол 60O (рис. 2.3а). Несмотря на свою простоту, в природе такая решетка встречается редко. Гораздо же чаще встречается несколько более сложная на первый взгляд структура.
Рис. 2.
3. Элементарная ячейка гексагональной и гексагональной плотноупакованной решетокГексагональная плотноупакованная решетка, сокращенно ГПУ, отличается от простой гексагональной тем, что в центр объема каждой второй треугольной призмы помещен дополнительный узел (рис. 2.
3б). При этом весь кристалл оказывается составлен из правильных тетраэдров. Это накладывает строгое условие на соотношение между высотой призмы c и длиной ее основания a: c/a = {8/3}1/2. Хотя решетки с другим близким к этому значением c/a часто рассматривают как слабодеформированный вариант ГПУ. Плотноупакованными называются решетки, в которых при заданном минимальном расстоянии между узлами достигается максимальная концентрация узлов в единице объема. Иногда такую упаковку называют плотной упаковкой твердых шаров.При этом каждый узел (или шар) имеет ровно 12 ближайших соседей, а весь объем кристалла распадается на правильные тетраэдры, вершины которых лежат в узлах решетки. Оказывается, что можно построить бесконечное множество плотноупакованных решеток. Но наиболее известны две самые простые --- кубическая гранецентрированная и гексагональная плотноупакованная. Можно проверить, что ГЦК решетка является плотноупакованной, хотя для того, чтобы пересчитать ближайших соседей, а тем более, чтобы представить себе ГЦК решетку как множество правильных тетраэдров нужно неплохое пространственное воображение.
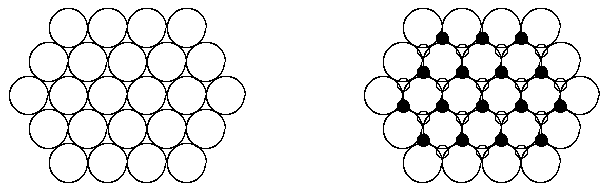
Рис. 2.
4. Плотноупакованный слой и возможные способы прилегания к нему соседних слоев (мелкие закрашенные и незакрашенные окружности)Чтобы построить любую плотноупакованную решетку, начнем с плотноупакованного слоя (рис. 2.
4а). Когда мы зафиксировали на плоскости любые два соседних узла, положение остальных узлов (проще представлять шаров) определяется однозначно. Нужно просто добавлять каждый шар так, чтобы он лежал на плоскости и касался, как минимум, двух соседних. При этом, когда вся плоскость покроется шарами, каждый шар будет касаться шести соседей. Взаимное же расположение плотноупакованных слоев определяется двузначно (рис. 2.4б).Узлы одного слоя образуют множество правильных треугольников, каждый из которых мог бы быть основанием правильного тетраэдра, в четвертой вершине которого расположен узел соседнего слоя. Но только половина таких треугольников может быть использована узлами одного соседнего слоя.
Если два слоя, прилегающих с разных сторон к данному, используют в качестве основания тетраэдров один и тот же набор треугольников, то получается гексагональная плотная упаковка, если всегда разные --- то кубическая гранецентрированная. Хотя разглядеть в такой структуре ГЦК достаточно трудно. Более сложный закон чередования порядка прилегания соседних слоев приводит к еще более сложным решеткам.
Кристаллическая решетка алмаза
несколько сложнее рассмотренных выше простой, объемно- или гранецентрированных решеток, поэтому уделим ей особое внимание.Эта решетка должна обладать следующим свойством: каждая частица имеет 4 ближайших соседей, находящихся на равном расстоянии и угол между направлениями на любые два из них равен
120O. Таким образом, каждая частица находится в центре правильного тетраэдра с вершинами в ее соседях.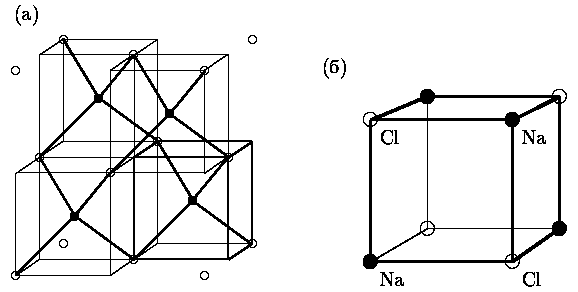
Рис. 2.
5. Структура алмаза (а) и кристалла NaCl (б)На словах структуру алмаза можно описать так. Это гранецентрированная кубическая решетка с четырьмя дополнительными частицами (рис. 2.
5а). Их положение определим следующим образом. Разобьем кубическую ячейку на восемь маленьких делением ее тремя плоскостями, параллельными граням и проходящими через центр ячейки. Из полученных восьми кубиков выберем четыре не имеющие общей грани, переходящие один в другой при отражении относительно ребер кубиков. В центр объема каждого из этих 4 ``восьмушек'' поместим по частице. Иначе эту решетку можно представить как две гранецентрированные решетки, смещенные одна относительно другой на четверть главной диагонали куба.Для получения этой структуры к ячейке гранецентрированной кубической решетки нужно добавить следующие узлы:
Pi = { [[1/4, 1/4, 1/4]], [[1/4, 3/4, 3/4]], [[3/4, 1/4, 3/4]], [[3/4, 3/4, 1/4]] }
Несложно проверить приведенные выше основные свойства решетки. Расстояние между ближайшими соседями равно 31/2 a /4$.
Таблица 2.1. Некоторые характеристики основных типов кристаллических решеток
|
Характеристика |
Тип решетки |
||||
|
ПК |
ОЦК |
ГЦК |
ГПУ |
алмаз |
|
|
Объем элементарной ячейки |
a3 |
a3 |
a3 |
a3 / 21/2 |
a3 |
|
Число узлов в ячейке |
1 |
2 |
4 |
2 |
8 |
|
Число узлов ячейки на единицу объема |
1 / a3 |
2 / a3 |
4 / a3 |
2 / a3 |
8 / a3 |
|
Число ближайших соседей |
6 |
8 |
12 |
12 |
4 |
|
Расстояние между ближайшими соседями |
a |
a 31/2/2 |
a / 21/2 |
a |
a 31/2/4 |
|
Число соседей, следующих за ближайшими |
12 |
6 |
6 |
2 |
6 |
|
Расстояние до соседей, следующих за ближайшими соседями |
a 21/2 |
a |
a |
a (8/3)1/2 |
a / 21/2 |
Некоторые вещества состоят из атомов разных типов. Это могут быть различные химические соединения и сплавы. Рассмотрим для примера кристалл обычной поваренной соли
Na Cl (рис. 2.5б). Его структуру можно представить как простую кубическую решетку, в узлах которой чередуются атомы Na и Cl. Это представление более наглядно, но такая ячейка не является элементарной, поскольку при переносе ее на элементарные трансляции атомы Na переходят в атомы Cl и наоборот.Более корректно рассматривать эту структуру как состоящую из двух кубических гранецентрированных решеток
Na и Cl, смещенных на половину вектора элементарной трансляции.[1] А. А. Кацнельсон, ``Введение в физику твердого тела'', Изд-во Московского университета, 1984
[2] Ч. Киттель, ``Введение в физику твердого тела'', Госуд. изд-во физико-математической литературы, Москва, 1962, Глава 1.
[3] Ч. Киттель, ``Элементарная физика твердого тела'', Москва, ``Наука'', 1965, Глава 1.
[4] В. В. Балашов, ``Строение вещества'', Изд-во Московского университета, 1993
Данная работа поддержана грантом РФФИ--2000, проект 00--02--17207. Демонстрационную версию программы можно найти на Web--страничке кафедры физики атомного ядра и квантовой теории столкновений сайта НИИЯФ МГУ: http://www.sinp.msu.ru/np_chair.php3. Договориться о регистрации и условиях использования программы и получить регистрационный код можно по тел. 939--25--13 или E-mail: bibikov@monet.npi.msu.su